Taylor Series

This is the Taylor Series.

Presented by Caroline Albertson, Lexi Doudera, and Eben Kopp.

On the Thirtieth of June, in the year of 2013, as we know it.

The concept of the Taylor Series was formally introduced by the mathematician Brook Taylor in 1715.

If the Taylor series is centered at zero, then that series is also called a Maclaurin series, named after the Scottish mathematician Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. 

The Taylor series is commonly used to approximate a function, using the series specifically. A Taylor polynomial is any finite number of initial terms of the Taylor series of a function. The Taylor series of a function is the limit of that function's Taylor polynomials, provided that the limit exists.

When you are approximating a function, the Taylor series goes like this:

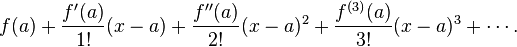
Where it can be written as a more compact notation:

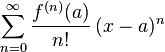
where n! denotes the factorial of n and ƒ ⁽ⁿ⁾(a) denotes the nth derivative of ƒ evaluated at the point a. 

Example:

We will approximate the graph of  using the Taylor series. 

As the Taylor polynomial increases with each degree, it approaches the correct function.

 

This graph shows  and it's Taylor approximations, polynomials of degree 1, 3, 5, 7,9, 11 and 13.

Here is another example of the Taylor series and the graph of e^x.

This graph shows e^x and it's Taylor approximations, polynomials of degree 1, 2, 3, 4, 5, 6, 7, 8, and 9.

Here are the calculations which go along with the graph:

Now that you know what the Taylor series is, here is a video which shows just how much we love math:

http://www.youtube.com/watch?v=FjGk4QY31Pc&feature=autoshare

Here is a link to our quiz:

https://docs.google.com/forms/d/1N1mYLjqP0XA6LuSDvQCPUIV_jHZxd9FSJHoiJrw56IA/viewform