Today, we learn how to use double integrals to calculate the surface area of regions of three dimensional surfaces. In middle school and highschool geometry class, we learned how to find the areas of polygons, and this in turn allowed us to calculate the surface areas of a variety of three dimensional shapes composed of four or more polygon faces (boxes, pyramids, platonic solids, ect. Even–with a little cleverness–cylinders and cones). This past semester, we learned how to find the area of a two dimensional shape bounded by two or more functions using integrals, and also the surface are of a rotation of a function. But what if you want to find the surface are of a multivariable function (f(x,y) a.k.a. surface)? Turns out, just as two integrals are required to calculate the volume under a surface, so too do we use a double integral to calculate this.
Whenever we integrate, we are actually summing an infinite number of infinitely small pieces of what we want to calculate. For example, when calculating the area under the curve of a function, we sum up rectangles with lengths which vary with the function value and infinitely small widths. But we already know this, and it makes sense. Two weeks ago we learned about the arc length of a function, and how that is calculated.
We arrived at this equation using Pythagoras and his fanciness, and what this equation is actually doing is summing up an infinite number of infinitely small hypotenuses to get the nonlinear length of the function. Now, this equation helps us in two dimensions (it is called a Cartesian PLANE after all), but when we expand our frame of context to three dimensions, the equivalent to what is in effect the perimeter of a single variable function is the surface area of a function in two variables. So instead of summing little tiny hypotenuses (one dimensional lines), we must sum little tiny polygons (two dimensional shapes). Notice the trend of increasing dimensions? It's that easy! The two dimensions which we want these polygons to have are a small dx and a small dy, and we want them to cast a "shadow", if you will, on the x-y plane which is square (dx and dy both approach 0 at the same rate). But when the surface is not perfectly horizontal, the shapes themselves are not squares, but rather parallelograms. So thus, we want to integrate the areas of all these parallelograms twice: once with respect to the y dimension, once to x dimension.
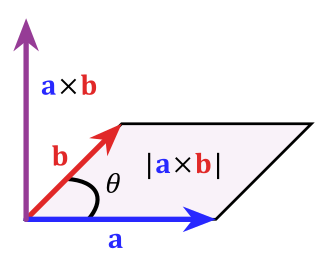 But what is the formula for the areas of these parallelograms, you might ask. This is where it gets a little bit tricky. Turns out, that there is a handy formula for the areas of these shapes, but it gets into vector math, which can be a bit confusing at first. The area of a parallelogram can be expressed as the magnitude of the cross product of the vectors (lets call them a and b) which make up two of its adjacent sides:
But what is the formula for the areas of these parallelograms, you might ask. This is where it gets a little bit tricky. Turns out, that there is a handy formula for the areas of these shapes, but it gets into vector math, which can be a bit confusing at first. The area of a parallelogram can be expressed as the magnitude of the cross product of the vectors (lets call them a and b) which make up two of its adjacent sides:Since we will be summing these areas later on, we call each individual area dA. Now, I don't want to get too far into an explanation of the calculation of a cross product (more information on those here, but the idea is that the resultant vector has the components shown below.
Which can be simplified…
Notice the partial derivatives–we learned about these when we were first introduced to multiple integrals, but more information on them can be found here. So now, we know have an expression for all the little cross product vectors in unit vector notation, it is simple to find the magnitudes:
Note that because the terms under the radical are squared, the negatives drop out. And now, we are all ready to sum the areas up with integration giving the general equation for surface area of a function in two variables:
Now, while this equation can help you set up a double integral , evaluating this integral can be a bit of a pain sometimes. And unfortunately, our calculators don't really like to do integrals dealing in two variables, so for now, we can very easily be stumped (for instance by the function f(x,y) = x^2 +y^2), but that is not the point! WolframAlpha can help with that, and if you're like me, you will look forward to learning how to deal with these baddies in the next couple of years!
Let me leave you with an example of using this formula to calculate the area of a manageable planar function:
Find the surface area of the part of the plane 

Remember that the first octant is the portion of the xyz-axis system in which all three variables are positive. Let’s first get a sketch of the part of the plane that we are interested in.
We’ll also need a sketch of the region D.
Remember that to get the region D we can pretend that we are standing directly over the plane and what we see is the region D. We can get the equation for the hypotenuse of the triangle by realizing that this is nothing more than the line where the plane intersects the xy-plane and we also know that 







Notice that in order to use the surface area formula we need to have the function in the form 



The limits defining D are,
The surface area is then,
[source]