 |
| His Eminence Sir William |
a. long division
b. substitution
BREAK
Apparently there was not supposed to be a scribe post for Tuesday or Wednesday, so we will continue on Thursday.
If you are having trouble with Integration by Substitution when you change the limits of the integral from terms of x to terms of u, check out this video. It particularly helps with IW#1, problems 54, 55, 59, and 71.
THURSDAY:
Today we began by reminding the whole class to sign up for their AP Calculus Exam. If you forget how to, you can go to the guidance office to figure that ish out.
Supercorrection follow-up tests came back in after that. Our class continues to improve on these tests each time! We proceeded to go over the answers to each question
1. Physics bums need to remember the superiority of radians.
2. Trapezoid Rule (remember area of a trapezoid)
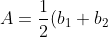h "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
The two bases are actually two heights in this problem set, and the height is correspondent to the width of each trapezoid.
3. Remember to divide the integral by the interval to get the average value.
4. a. nDeriv(v(t))
4. b. total distance:|\delta%20x} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
The absolute value sign accounts for areas between the curve and x axis that are negative (when the curve dips below the x axis).
4. c. Fundamental Theorem of Calculus:\delta%20t}=x(b)-x(a) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
In the problem set: a = 0, b = 5, x(0) = 4
So,
\delta%20t}+x(0)=x(5)\\\\\int_{0}^{4}{\sin{t^2}\delta%20t}+4=x(5)\\\\0.5279+4=x(5)\\\\x(5)=4.5279 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
5. Check your answer by deriving! If it didn't work, then try to figure out what was missing.
6. Any integral of an exponential function with base e will always include e raised to the original power in the answer. This can provide a good starting point for these problems. By taking the derivative of the integrand, you can identify which constants are necessary to transform the function into the integral.
7. Graph it!
8. Split apart the integral by Addition Rule and integrate!
9. a. Zero Rule of Integration
9. b. Order of Integration
9. c. Odd functions are symmetrical about the origin
9. d. Addition/Subtraction of Integrals
2000 AP Calculus Question 1
a. As a Sum of Rectangles, and, by extension, and integral
choose a base (a change in x)
then find your heights (height of upper function-height of lower function <= always positive)
^difference between two functions
set up your integral (upper function - lower function <= this changes depending on interval)
}\delta%20x "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
k = point of intersection, so the point where
(Solver, then integrate)
Small Break:
Golden Way: Finding area between any two curves
-g(x)|\delta%20x} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
^ensures that the height will always be positive
If there are three curves => you need multiple integrals
b. The volume of the solid when revolved around the x axis? What?!
1. Take representative rectangle (selection from area btw curves)
2. Revolve around axis to create washer/ CD shape.
3. find the area and then the volume.
Area of two concentric circles = area of larger - area of smaller
So, since the base e function is larger than the cosine function, and area of a circle = πr^2
-\pi%20(1-\cos{x}))}\delta%20x "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
This is advanced stuff though, we will cover it in more detail later. Feel no obligation to understand this at this juncture. We will ease into it.
IW#3 p. 399/ 2, 4, 10, 14
2. area btw
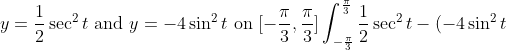}\delta%20t\\\\\\2\left(\int_{0}^\frac{\pi}{3}{\frac{1}{2}\sec^2{t}\text{%20}\delta%20t+4\int_0^\frac{\pi}{3}\sin^2{t}}\text{%20}\delta%20t\right)\\\\\\\int_{0}^\frac{\pi}{3}\sec^2{t}\text{%20}\delta%20t%20+%208\int_0^\frac{\pi}{3}\sin^2{t}\text{%20}\delta%20t "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
4. area between two vertical (think horizontal rectangles)
-(2y^2-2y)\right)}\delta%20y "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
= 4/3 or 1.33333....
10.
Watch out, you can solve for x or y on this one!
-(\sqrt{y})%20\right%20)%20\delta%20y\\\\\text{Or,%20}\int_0^1%20{x^2}\delta%20x+\int_1^2({2-x})\delta%20x "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
The second integral in the second one is just a right triangle, so use Pythagorus!
Answer: 0.83333333....
This area work can be tricky, but is is the exact same process as finding the combined area of two curves. The only difference is that we are using subtraction instead of addition. If you are still confused, then ask Patrick JMT. Visual Calculus does a great job showing step-by-step solutions to a number of "area between two curves" problems.
14. space between
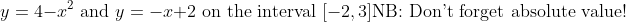
First: Determine dx or dy formula (think about the rectangles => vertical vs. horizontal)
-\left(-x+2%20\right%20)|}\delta%20x%20=%208.16666514 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
Without tech: find intersections and integrate with smaller function subtracted from the larger.
Intersections: (-1, 3) and (2,0)
-\left(-x+2%20\right%20)\right]}\delta%20x%20+\int_{-1}%20^{2}{\left[\left(-x+2%20\right%20)-\left%20(4-x^2%20\right%20)\right]}\delta%20x%20+\int_{2}%20^{3}{\left[\left%20(4-x^2%20\right%20)-\left(-x+2%20\right%20)\right]}\delta%20x "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
p. 401/ 49
Find the intersections:
x = 0.8241323....
Set up the integral:
\delta%20x=2\\\\k\int_{0}^a%20\left(\cos{x}-x^2%20\right%20)\delta%20x=1\\\\k\left[\sin{x}%20-\frac{x^3}{3}%20\right%20]_0^a=1\\\\k=\frac{1}{\sin{a}-\frac{a^3}{3}}\\\\k=1.826895097 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
Next scribe will be Gabe (Eddie dropped out).
THURSDAY:
Today we began by reminding the whole class to sign up for their AP Calculus Exam. If you forget how to, you can go to the guidance office to figure that ish out.
Supercorrection follow-up tests came back in after that. Our class continues to improve on these tests each time! We proceeded to go over the answers to each question
1. Physics bums need to remember the superiority of radians.
2. Trapezoid Rule (remember area of a trapezoid)
The two bases are actually two heights in this problem set, and the height is correspondent to the width of each trapezoid.
3. Remember to divide the integral by the interval to get the average value.
4. a. nDeriv(v(t))
4. b. total distance:
The absolute value sign accounts for areas between the curve and x axis that are negative (when the curve dips below the x axis).
4. c. Fundamental Theorem of Calculus:
In the problem set: a = 0, b = 5, x(0) = 4
So,
5. Check your answer by deriving! If it didn't work, then try to figure out what was missing.
6. Any integral of an exponential function with base e will always include e raised to the original power in the answer. This can provide a good starting point for these problems. By taking the derivative of the integrand, you can identify which constants are necessary to transform the function into the integral.
7. Graph it!
8. Split apart the integral by Addition Rule and integrate!
9. a. Zero Rule of Integration
9. b. Order of Integration
9. c. Odd functions are symmetrical about the origin
9. d. Addition/Subtraction of Integrals
END OF SUPERCORRECTION REVIEW
THE FINAL PROBLEM!
Area bounded by two curves?
Not all math is nice, some is sketchy.
a. As a Sum of Rectangles, and, by extension, and integral
choose a base (a change in x)
then find your heights (height of upper function-height of lower function <= always positive)
^difference between two functions
set up your integral (upper function - lower function <= this changes depending on interval)
k = point of intersection, so the point where
Small Break:
Golden Way: Finding area between any two curves
^ensures that the height will always be positive
If there are three curves => you need multiple integrals
b. The volume of the solid when revolved around the x axis? What?!
1. Take representative rectangle (selection from area btw curves)
2. Revolve around axis to create washer/ CD shape.
3. find the area and then the volume.
Area of two concentric circles = area of larger - area of smaller
So, since the base e function is larger than the cosine function, and area of a circle = πr^2
This is advanced stuff though, we will cover it in more detail later. Feel no obligation to understand this at this juncture. We will ease into it.
IW#3 p. 399/ 2, 4, 10, 14
2. area btw
4. area between two vertical (think horizontal rectangles)
= 4/3 or 1.33333....
10.
Watch out, you can solve for x or y on this one!
The second integral in the second one is just a right triangle, so use Pythagorus!
Answer: 0.83333333....
This area work can be tricky, but is is the exact same process as finding the combined area of two curves. The only difference is that we are using subtraction instead of addition. If you are still confused, then ask Patrick JMT. Visual Calculus does a great job showing step-by-step solutions to a number of "area between two curves" problems.
14. space between
First: Determine dx or dy formula (think about the rectangles => vertical vs. horizontal)
Without tech: find intersections and integrate with smaller function subtracted from the larger.
Intersections: (-1, 3) and (2,0)
p. 401/ 49
Find the intersections:
x = 0.8241323....
Set up the integral:
Next scribe will be Gabe (Eddie dropped out).
No comments:
Post a Comment