Mr. O'Brien's 2012-13 Period 2 AP Calculus: Scribe Post 3/11/13

We walked into class today and, being the devoted math students we are, were thrilled to see today's goal on the board accompanied by three juicy problems to help us acquire this new and stimulating knowledge. You can imagine my jubilance when I was told I had the honor of scribing for today's class and recording each and every happening on this glorious day of mathematics. The whole class was enthusiastic to dig right into these three succulent example problems, but we were forced to put our excitement on hold, as Sarah had a question about last night's IW (which we should all probably get cracking on).

Sarah's question was this: does it matter whether we look at an area problem with vertical rectangles or horizontal rectangles?

OB decided to answer this question by taking a look at question 3 on page 399, which told us to find the area of this ugly thing below. OB sketched it up on the board and plotted some points by plugging numbers into the equation.

We decided to try solving this problem by using both horizontal rectangles and vertical rectangles. OB pointed out that if we use horizontal rectangles, we are summing rectangles from y=0 to y=1 on the y-axis and if we use vertical rectangles we are summing rectangles from x=0 to x=1 on the x-axis. The working for both methods is shown below:

Horizontal: Vertical:

Same-Same!

The lesson to learn from this problem is that areas can be found both with horizontal and vertical rectangles, but sometimes one is easier than the other.

From here we moved onto volume and looked at the first problem in our set of three:

When we sketch this area, we get something that looks like:

OB pointed out that here we are "summing discs" that look like the one above that have a radius of x^2-4x+5 and a thickness of dx. To find the volume of the resulting shape, we can simply sum up the volumes of all these discs, shown below (the volume of a disc is its area multiplied by its thickness)

Fully satisfied with this answer, we moved onto the next problem:

We're summing discs again, but this time the discs have a hole in the middle! They're washers (or pineapple slices, or bagel chips, etc)! How do we find the area of a washer? The area of the big circle minus the area of the little circle. The calculus working for this problem is shown below:

After finding this solution, we went on a bit of a tangent about the volume of a cone. We all know (questionable) the volume of a cone is (πhr^2)/3, but it has never really been proven to us until now because those silly geometry teachers don't know calculus! Work is shown below:

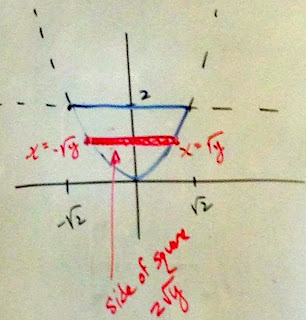
From here we moved on to our last and final problem of the day:

Our representative rectangle looks like this, with a length of 2√y. This means that each square will have side lengths of 2√y, and therefore an area of (2√y)^2.

To find the volume we simply sum up the areas of all the squares:

This is all well and nice, but what if the cross-sections were something other than squares, like equilateral triangles? We figured this one out as well.

OB proclaimed that we can use any cross-section as long as it can be described. In other words, as long as we can find the cross-sectional area of each slice, we can find the volume of the entire shape.

After working through these three tough problems, OB gave us ten minutes to watch the videos he posted on "Volume Links" to help us visualize some of these shapes. Some watched the videos. Others discussed the AP Lit assignment.

Once the ooh-ing and ahh-ing from the videos had died down, OB gave us the rest of class to work on IW #4.

Here is my copy of IW #4 after those 10 minutes of hard work: