Scribe Post 3/13/13

Today we began class with a quiz covering IW's 1-4. Then Mr. O'Brien reminded us that the deadline to register for AP Tests is this Friday, but since there's no school on Friday, your best bet is to have the paperwork handed in on Thursday. 

Next we looked at a video by ViHart about a mysterious number called Wau. She talked about all of wau's properties which were numerous. There was a bit of confusion in the room until we realized wau was just 1. 

Then O'B spoke some pretty powerful words: "We're done. We've finished calculus." Well, we've almost finished calculus. This led O'B into a discussion about the weeks between now and the AP Test. All of this info can be found on the iCal, but I'll summarize: 

- O'B is leaving and will not be here next week. IW 6 and 7 will be assigned while he is away. They are a set of FRQ's with answers. Make sure you actually do the FRQ's because there will be a quiz the Friday (March 22) he gets back on IW 5 and the FRQ's. There will be NO number changes, which means we can't use notes.

- If you have questions about IW 6 or 7, just post them up and O'B will get to them as soon as he can. We will have 3 hours of in class time to get these done. Thats double the amount of time we need. 

-March 26 (tuesday): We have a test. IW's 5-8 are due. 

-March 29 (friday): Supercorrections are due. 

- April 3: The first grade of Q4 will be the follow up test!

- Aril 5: The first quiz of Q4 will be trig values. This is not timed and is re-takable up to 100%

-April 9 and 11: Quizzes on FRQ's. NO number changes. Do IW and you'll be set. Closed notes.

-April Break: Optional FRQ's

- April 24 and 26: Multiple choice section of full AP practice test

-April 30 and May 2: FRQ section of full AP practice test

-May 6: Supercorrections due for the above test

-Tuesday May 7: Deadline for all late work. 

-Wednesday May 8: AP TEST

- No work will be accepted after the AP test. It's a waste of everyone's time. We will then do a project as our final exam and we are allowed to work in partners or threesomes. 



Now on to IW 5. Although the link for this IW can be found on the ical, make sure you write all the answers out in your notebook, not just on the handout. 

IW#5 Question 31:

Find the volume of the solid generated by revolving the region bounded by the parabola y=x^2 and the line y=1 about

(a) the line y=1
(b) the line y=2
(c) the line y=-1

Here is a graph of this scenario courtesy of Connor Lane: 

A)
So, in part a, we are revolving this around the line of y=1 which happens to be one of the boundaries of the shaded region. This means that when we rotate it, it's radius will just be the distance between the line y=1 and the curve y=x^2. So, this gives us:

Notice that the limit is just from 0 to 1. Even though the shaded region goes from -1 to 1, we compensate by doubling the integral since it is symmetric about the y axis. 

B)
Okay, so now we're rotating it about the line y=1. When we take a cross section of this, it is going to give us a washer. This means we need to subtract the inner circle from the outer circle to get the area of the washer, then multiply it by that small thickness, dx. 

The first term of the integrant is the big radius, while the second is the small radius, which then become the big circle and the small circle, respectively when you multiply them by pi and square them. Multiple all this by that small width to get the area!

C) 
Now we are rotating it about the line y=-1. In part B, the outside of the solid had a curve to it, while the inside was flat. It made a roller blade-esque wheel. However, now the outside radius remains the same, while the inside radius is changing. So, we have to take the big radius that is formed between the line y=1 and y=-1 and subtract the little radius from it. This little radius is changing and is formed between y=x^2 and y=-1

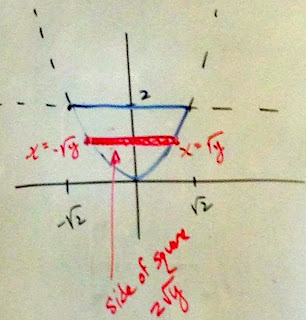
Next we looked at #1 from IW 5

Find the volume of the solid with semicircular cross sections whose base is in the xy-plane between the x-axis and the curve y=sqrt(x) over [0,9]. See the visualization here.

Remember that the area of a semi circle is just half of the area of a circle. So, (1/2)πr^2.

Here is a graph of what we're looking at:

So, as you can see, the diameter will be changing. And remember, we're interested in the radius so we'll have to split the diameter in two! This gives us:

Scribe Post 3/11/13

We walked into class today and, being the devoted math students we are, were thrilled to see today's goal on the board accompanied by three juicy problems to help us acquire this new and stimulating knowledge. You can imagine my jubilance when I was told I had the honor of scribing for today's class and recording each and every happening on this glorious day of mathematics. The whole class was enthusiastic to dig right into these three succulent example problems, but we were forced to put our excitement on hold, as Sarah had a question about last night's IW (which we should all probably get cracking on).

Sarah's question was this: does it matter whether we look at an area problem with vertical rectangles or horizontal rectangles?

OB decided to answer this question by taking a look at question 3 on page 399, which told us to find the area of this ugly thing below. OB sketched it up on the board and plotted some points by plugging numbers into the equation.

We decided to try solving this problem by using both horizontal rectangles and vertical rectangles. OB pointed out that if we use horizontal rectangles, we are summing rectangles from y=0 to y=1 on the y-axis and if we use vertical rectangles we are summing rectangles from x=0 to x=1 on the x-axis. The working for both methods is shown below:

Horizontal:                                                                                           Vertical:

Same-Same!

The lesson to learn from this problem is that areas can be found both with horizontal and vertical rectangles, but sometimes one is easier than the other.

From here we moved onto volume and looked at the first problem in our set of three: 

When we sketch this area, we get something that looks like:

OB pointed out that here we are "summing discs" that look like the one above that have a radius of x^2-4x+5 and a thickness of dx. To find the volume of the resulting shape, we can simply sum up the volumes of all these discs, shown below (the volume of a disc is its area multiplied by its thickness)

Fully satisfied with this answer, we moved onto the next problem:

We're summing discs again, but this time the discs have a hole in the middle! They're washers (or pineapple slices, or bagel chips, etc)! How do we find the area of a washer? The area of the big circle minus the area of the little circle. The calculus working for this problem is shown below:

After finding this solution, we went on a bit of a tangent about the volume of a cone. We all know (questionable) the volume of a cone is (πhr^2)/3, but it has never really been proven to us until now because those silly geometry teachers don't know calculus! Work is shown below:

From here we moved on to our last and final problem of the day:

Our representative rectangle looks like this, with a length of 2√y. This means that each square will have side lengths of 2√y, and therefore an area of (2√y)^2.

To find the volume we simply sum up the areas of all the squares:

This is all well and nice, but what if the cross-sections were something other than squares, like equilateral triangles? We figured this one out as well.

OB proclaimed that we can use any cross-section as long as it can be described. In other words, as long as we can find the cross-sectional area of each slice, we can find the volume of the entire shape.

After working through these three tough problems, OB gave us ten minutes to watch the videos he posted on "Volume Links" to help us visualize some of these shapes. Some watched the videos. Others discussed the AP Lit assignment.

Once the ooh-ing and ahh-ing from the videos had died down, OB gave us the rest of class to work on IW #4.

Here is my copy of IW #4 after those 10 minutes of hard work:

3/12/13 40 min period:

During the 40 minute period, we went over questions from the IWs. Solutions are below:

p410 / 9

p410 / 19

p410 / 23

NEXT SCRIBE IS EBEN

Volume links

Volume of revolution

Volume of revolution with a hole

Volume with known cross sections

Volume with known cross sections applet (needs plug-in but worth it...)

Volume with known cross sections image gallery

U-substitution practice

Practice problems with solution for u-substitution:

http://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/usubdirectory/USubstitution.html#PROBLEM 1

Scribe Post 5-8 March

Knowing that the class was to begin with a thrilling Supercorrection Follow-up Test, all students merrily frolicked into room 219 as Crockett played "Concerning Hobbits." This joyful tune made many a happy face on this fateful day of integration. Proceeding with gusto, the class delved into the test from 33 minutes past the hour of nine until time ran out 13 minutes after ten o'clock. The scribe post of the exceptionally affluent and widely respected Sir William Billiam Shilliam Dilliam Strongclaw Proudfoot Covenhoven III (seen below) was then thoroughly analyzed and appreciated before moving on to the topic at hand: Integration by Substitution.

His Eminence Sir William

Task 1: Solve the following



a. long division



b. substitution

BREAK

Apparently there was not supposed to be a scribe post for Tuesday or Wednesday, so we will continue on Thursday.

If you are having trouble with Integration by Substitution when you change the limits of the integral from terms of x to terms of u, check out this video. It particularly helps with IW#1, problems 54, 55, 59, and 71.

THURSDAY:

Today we began by reminding the whole class to sign up for their AP Calculus Exam. If you forget how to, you can go to the guidance office to figure that ish out.

Supercorrection follow-up tests came back in after that. Our class continues to improve on these tests each time! We proceeded to go over the answers to each question

1. Physics bums need to remember the superiority of radians.
2. Trapezoid Rule (remember area of a trapezoid)
                  
The two bases are actually two heights in this problem set, and the height is correspondent to the width of each trapezoid.

3. Remember to divide the integral by the interval to get the average value.

4. a. nDeriv(v(t))
4. b. total distance: 
The absolute value sign accounts for areas between the curve and x axis that are negative (when the curve dips below the x axis).
4. c. Fundamental Theorem of Calculus: 
           In the problem set: a = 0, b = 5, x(0) = 4
           So,

            

5. Check your answer by deriving! If it didn't work, then try to figure out what was missing.

6. Any integral of an exponential function with base e will always include e raised to the original power in the answer. This can provide a good starting point for these problems. By taking the derivative of the integrand, you can identify which constants are necessary to transform the function into the integral.

7. Graph it!

8. Split apart the integral by Addition Rule and integrate!

9. a. Zero Rule of Integration
9. b. Order of Integration
9. c. Odd functions are symmetrical about the origin
9. d. Addition/Subtraction of Integrals

END OF SUPERCORRECTION REVIEW

THE FINAL PROBLEM!

Area bounded by two curves?

Not all math is nice, some is sketchy.

2000 AP Calculus Question 1

a. As a Sum of Rectangles, and, by extension, and integral
     choose a base (a change in x)
     then find your heights (height of upper function-height of lower function <= always positive)
          ^difference between two functions
      set up your integral (upper function - lower function <= this changes depending on interval)
            
        k = point of intersection, so the point where  (Solver, then integrate)

Small Break:

   Golden Way: Finding area between any two curves
      
          ^ensures that the height will always be positive
   If there are three curves => you need multiple integrals

b. The volume of the solid when revolved around the x axis? What?!
      1. Take representative rectangle (selection from area btw curves)
      2. Revolve around axis to create washer/ CD shape.
      3. find the area and then the volume.
  Area of two concentric circles = area of larger - area of smaller
  So, since the base e function is larger than the cosine function, and area of a circle = πr^2
           
This is advanced stuff though, we will cover it in more detail later. Feel no obligation to understand this at this juncture. We will ease into it.

IW#3 p. 399/ 2, 4, 10, 14

2. area btw
      




4. area between two vertical (think horizontal rectangles)


            = 4/3 or 1.33333....

10. 
     Watch out, you can solve for x or y on this one!
          
          The second integral in the second one is just a right triangle, so use Pythagorus!
          Answer: 0.83333333....

This area work can be tricky, but is is the exact same process as finding the combined area of two curves. The only difference is that we are using subtraction instead of addition. If you are still confused, then ask Patrick JMT. Visual Calculus does a great job showing step-by-step solutions to a number of "area between two curves" problems.

14. space between
       
First: Determine dx or dy formula (think about the rectangles => vertical vs. horizontal)
          
Without tech: find intersections and integrate with smaller function subtracted from the larger.
        Intersections: (-1, 3) and (2,0)



p. 401/ 49


Find the intersections:

x = 0.8241323....

Set up the integral:



Next scribe will be Gabe (Eddie dropped out).