Number 17 first asked us to sketch a slope field for the differential equation
.gif) , which had already done because we're such exemplary students.
, which had already done because we're such exemplary students. .JPG) |
| Ignore the drawn-in parabola for now. |
For the second part of "B" we sought to estimate the value of f(1.2) with our brand spanking new tangent line equation. So we plugged it in and got 1.2.
Part "B" aside, we moved onward toward grander horizons. Those horizons namely being part "C". "C" asked us for the "particular solution y = f(x) to the differential equation with the initial condition f(1) = 1." And then to use that function to find the real f(1.2) , not that impostor estimate. (Note to self: The Impostor Estimates... good band name?). To do this properly, we used "separation of variables" to find the integral. Separation of variables is when you use algebra to manipulate a differential equation into having all the x's on one side and the y's on another. Then, you throw integral signs on it.
.JPG) |
| (Correction: it's spelled "integrand") |
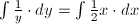.gif) we are just finding the antiderivative of the
we are just finding the antiderivative of the .gif) . We can use log properties to make both sides exponents with bases of e, eliminating the natural log from the equation and getting
. We can use log properties to make both sides exponents with bases of e, eliminating the natural log from the equation and getting.gif) So where to from here? That variable "C" is still a mystery, so we need to find that. To do this, it is vital to remember that this function coincides with the point (1,1). Subbing in our "y" and "x" values, we find the equation becomes
So where to from here? That variable "C" is still a mystery, so we need to find that. To do this, it is vital to remember that this function coincides with the point (1,1). Subbing in our "y" and "x" values, we find the equation becomes.gif) which then becomes
which then becomes.gif) in order to eliminate e from the equation. This leaves us with
in order to eliminate e from the equation. This leaves us with.gif) meaning
meaning . Subbing that back into the equation, we get
. Subbing that back into the equation, we get  Based on this equation, f(1.2)=1.116.
Based on this equation, f(1.2)=1.116.Part "D" asked us to compare our phony estimate with the real answer. So we did. Based on our razor sharp skills of deduction, we deduced that 1.2 is greater than 1.116. Part "E" then asked if we had over or underestimated. Again, our obsidian-edged mental acuity brought us to the conclusion that we had overestimated. After some jumping around by O'B, we realized that this (the conclusion, not the jumping) was due our differential equation being concave up (yes, we finally went back to that slope field)! Thus the tangent line would always be below the function.
Problem 17 complete, we moved on to 18 and promptly realized we could use the same sweet moves to split up the differential equation and find the constant. Here's a picture:
Where "C" is circled in the middle of the working, we ran into a property of constants that we may not have gone over before. As is apparent, other variables change, but the variable "C" is not affected. This is because a manipulated constant is still just a random constant, so we can stick with "C" as a representative letter.
With both 17 and 18 aside, and no more questions from the brilliant Advanced Placement™ students, O'B handed out another sheet: Exploration 7-2 and 7-3. We began with the first two problems on the 7-2 side.
We found the differential equation by translating this from English to Math Language (the one language Google Translate still doesn't encompass). First, because there was an instantaneous rate of change involved, we needed a derivative. So we plunked a lil' dM/dt onto the paper (M referring to money, t referring to time). Then we saw that the rate of change in money was proportional to the amount of money. This meant that we could put the variable "M" on the other side of the equation as well and get the proportionality. Finally, there needed to be a constant rate at which the money was coming in, so we assigned "k" to that job. It looked something like this:.gif)
.gif)
But then of course #2 told us to "Separate the variables in the differential equation", and then to "integrate both sides with respect to t. And THEN transform the integrated equation so that the amount of money was expressed explicitly in terms of time. So we split it up:
And solved it in steps...
M is absolute because ln(-x) and ln(x) have the same derivative.
But we can strip it away when we realize we aren't dealing with negative money.
There's our answer! And a little sharp thinking will let us realize that OMG, we just derived A=Pe^rt, that crazy compound interest formula from last year! Yay!
Finally, we looked at the case of Ira Member (HA!) a young man who wants to predict how many people's names he remembered at a reception. #nolife #butactuallyhasalifebecausehegetsinvitedtococktailpartieswherehemeets100peopleanhour We can help Ira out by finding a function for number of names he remembers. We let
- R=rate at which he meets people per hour (a constant)
- t=number of hours at reception
- y=number of names remembered
- dy/dt=rate at which names are remembered
- And remember (HA!): the rate at which he forgets is proportional to y.
"So what are we trying to find?" asked the Cluester. Sometimes, he explained, words don't conform into mathematical perfection immediately. But after much discussion and throwing around of terms such as "derivative", "differentiation", "antidisestablishmentarianism", and "time", the class decided that what poor Ira really needed to know was the rate at which he would remember names. Could that rate be represented by the expression dy/dt? YES IT COULD. We then decided that that rate was equal to the rate at which he met people combined with the rate at which he forgot names, which was represented as -ky. Thus we had.gif) which we found we could solve through separation of variables:
which we found we could solve through separation of variables:
.gif) which we found we could solve through separation of variables:
which we found we could solve through separation of variables:
t=0 and y=0, so
With given values from problem:
And thus we end up with our final equation:
We can graph this equation to find out Ira's "terminal remembrance velocity"–the highest number of people Ira can remember regardless of how many bajillions of people he meets.
Looks like somewhere around 250.
In the last step, the constant seemingly disappears this is due to the fact that at the beginning of the reception, Mr. Member has not met anyone and no time has passed. Thus, y=0 and t=0, and thus the constant is 0 as well. Multiplication with that zero takes out the messy e value from the equation, leaving the simple equation R = C. This equation translates roughly into English as "At the beginning of the party, the rate at which Member meets people per hour is equal to the number he will remember given the time." By subbing in R for C, we managed to put the function in more comprehensive terms.
Extra links for the mathematically curious/confused:
- Actual applications for differential equations: radioactive decay, population dynamics.
- Didn't understand this post? Neither did I. These may help, although the topic seems to revolve fairly heavily on antiderivatives, which we've kind of solidified.
- As the midterm looms, this may help as a review. A quick memory jog.
- All the answers to IWs #1 and #2.
First, a scribe mistake was corrected (see the very long set of LaTex equations above.) The class then worked on IW #2 for the rest of the period. Here is help for #3.
Also, all the answers to IW #1 and #2 are online here.
That is all.
(The next scribe is Scotty.)
.gif)
.gif)
.gif)
.gif)
.gif)
.JPG)
.JPG)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.JPG)
.JPG)
No comments:
Post a Comment