① Recap the connection between acceleration, velocity, and speed.
② Understand a Riemann Sum
③ Begin to understand a definite integral
Today we started class with Mr. O'Brien explaining the presence of a video camera in one corner of the room (he might be sending a video of our class in action as part of an application for the Presidential Teacher's Award). Also, Mr. Bode was supposed to visit our class, so to look extra smart, we considered devising a plan in which everyone raises their hand after every question (but the people with the right answer would have a code signal to show Mr. O'Brien who to call on).
We then took a 15 minute FRQ quiz on motion and the relationships between velocity, speed and acceleration (closed notes, calculator ok).
① After the quiz, we checked our answers to IW#5 (here are the answers!) and talked a little more about yesterday's AP Calculus Poll o' the Day.
Our class: 9 "True", 8 "False"
Period 4: 4 "True", 7 "False"
Why did we get different ratios? What's the right answer? Well, this is a "sometimes, always, never question". That is, sometimes when an object has a negative acceleration, it is slowing down,
 |
| From situation 4, IW#5, unit 4 (line refers to speed) |
and sometimes when the acceleration is positive, the object is slowing down too.
 |
| From situation 3, IW#5, unit 4 (line refers to speed) |
* To be clear, when we say "slowing down", we mean the speed (that is, the absolute value of velocity) is decreasing.
② Next, we formed groups, and Mr. O'Brien handed out a worksheet called "Exploration of Riemann Sums". Some of us got a little stuck, so Mr. O'Brien asked, "Is there a middle school concept we need? Adding? Slope? NO!
distance = speed × time
*Oh, totally forgot that actually....
That allowed our class to complete sections a-d on the "Exploration of Riemann Sums" handout. Here are our answers (see descriptions in captions below).
That allowed our class to complete sections a-d on the "Exploration of Riemann Sums" handout. Here are our answers (see descriptions in captions below).
 |
| "A car is traveling so that its speed is never decreasing during a 10-second interval. The speed at various moments in time is listed in the table [above]." |
 |
| PART F: Note that despite getting slightly different values for the upper and lower estimates, all of the groups got the same value (30 ft/sec) for the error.... |
To understand Riemann Sums better, we looked at them graphically and analytically.
So, we suggested plugging the points given to us by the first table in the "Exploration of Riemann Sums" handout into Geogebra and used the amazing polyfit to create a function to represent the car's speed over time. BUT, Mr. O'Brien had already done that. Actually, he made a whole applet. In any case, the graph we suggested looked like this:
 |
| Coordinate points from "Exploration of Riemann Sums" handout graphed in Geogebra and connected using the polyfit function. |
Mr. O'Brien wrote on the board:
Somewhere on the graph is a visual representation of a Riemann Sum -- where would you find the Riemann Sum on the graph?
Ground Rules:
① Keep explanations to precalculus level
② No AP Physics bullying
* The red line is the lower estimate for the velocity over the allotted time intervals, while the blue line is the upper estimate.
How did we arrive at this graph? Let's take, for example the interval of 0 ≤ t ≤ 2 (where t is time in seconds). For the lower estimate, you could assume that the car is traveling at 30 ft/sec starting at t=0 right up until just before the t=2 mark. At that point, the speed would have to shoot up to 36 ft/sec. For the upper estimate over the same time interval, you could assume that the instant just after t=0, the car's speed shoots up to 36 ft/sec from 30 ft/sec, thus the car would spend almost all of the two seconds between t=0 and t=2 at 36 ft/sec.
Then we were asked what else the red and blue lines represented. Gabe suggested that Becca drew two possible speed graphs. In other words, she drew two plausible speed functions. We talked about how there are an infinite number of plausible functions between the two estimates, and how to two represented on the board in red and blue BOUND the infinite other options (think Squeeze Theorem everyone!). ONE of the other plausible functions was the one we created with the polyfit line that connected all of the data points:
Back to the main question-- that is, where to find the visual representation of the Riemann Sum from the graph. The Phyzards clearly already know what's going on, so Duncan goes up to the board and tries giving us a hint, but Mr. O'Brien isn't cooperating too well. Still, before Mr. O'Brien can stop him, Duncan draws THIS!
Okay! So Duncan drew the original polyfit line, and then filled in all the space between the line and the x-axis in the interval 0 ≤ t ≤ 2. The SUM of the area he filled in is 2 (seconds) × a number between 30 and 36 (since the speed in ft/sec between 0 ≤ t ≤ 2 is somewhere between 30 and 36 according to the table we're given in the "Exploration of Riemann Sums" handout. Hmmmm... 2 × 30 = 60 and 2 × 36 =72. Wait, those were the lower and upper estimates for the distance traveled in the first two seconds!
Then, Cal offers another hint:
Basically, he says that if you add up the total area between the upper and lower estimate lines, you'll get the total error-- that is, the maximum amount the approximation could differ from the exact distance.
Close up (error in the light blue):
At this point, the lightbulb went off. So! To find the Riemann sum from a graph, you have to figure out the (approximate) AREA of the space between the points on the original line and the x axis over the given interval of x values. In this way, you can find either extreme of the distance traveled, as you can either estimate that the car speeds up instantaneously after hitting each new interval, or that it stays at the speed for almost an entire interval before shooting up at the last minute (e.g. it stays at 30 ft/ sec for almost the entire 2 seconds over the interval 0≤ t ≤ 2).
In conclusion, the basic definition of a Riemann Sum (thanks wiki): "In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral." Foreshadow much?
FINAL THOUGHTS FOR THE DAY:
*****************************40 minute period (1/30/13)*****************************
Becca had an idea, so she went up to the board and drew this:
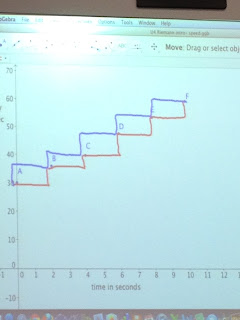 |
| Graphic representation of the lower and upper estimates for the velocities over the allotted time intervals (i.e. 0-2 seconds, 2-4 seconds, 4-6 seconds, etc.) |
* The red line is the lower estimate for the velocity over the allotted time intervals, while the blue line is the upper estimate.
How did we arrive at this graph? Let's take, for example the interval of 0 ≤ t ≤ 2 (where t is time in seconds). For the lower estimate, you could assume that the car is traveling at 30 ft/sec starting at t=0 right up until just before the t=2 mark. At that point, the speed would have to shoot up to 36 ft/sec. For the upper estimate over the same time interval, you could assume that the instant just after t=0, the car's speed shoots up to 36 ft/sec from 30 ft/sec, thus the car would spend almost all of the two seconds between t=0 and t=2 at 36 ft/sec.
Then we were asked what else the red and blue lines represented. Gabe suggested that Becca drew two possible speed graphs. In other words, she drew two plausible speed functions. We talked about how there are an infinite number of plausible functions between the two estimates, and how to two represented on the board in red and blue BOUND the infinite other options (think Squeeze Theorem everyone!). ONE of the other plausible functions was the one we created with the polyfit line that connected all of the data points:
This is probably a good time to talk about INTERVALS. In this problem, there are 5: Between 0-2, 2-4, 4-6, 6-8 and 8-10 seconds. It is important to note that having more intervals decreases the error. Imagine if there was only one interval for this problem (0-10 seconds). The error area would look like THIS!
Graphic representation of error (in pink) with 1 INTERVAL.
|
Alternately, the fewer the intervals, the smaller and smaller the area those error boxes would become until, eventually, they would blend right in with the original polyfit line.
Back to the main question-- that is, where to find the visual representation of the Riemann Sum from the graph. The Phyzards clearly already know what's going on, so Duncan goes up to the board and tries giving us a hint, but Mr. O'Brien isn't cooperating too well. Still, before Mr. O'Brien can stop him, Duncan draws THIS!
 |
| Duncan's graph represents the Riemann Sum where 0 ≤ t ≤ 2. |
Okay! So Duncan drew the original polyfit line, and then filled in all the space between the line and the x-axis in the interval 0 ≤ t ≤ 2. The SUM of the area he filled in is 2 (seconds) × a number between 30 and 36 (since the speed in ft/sec between 0 ≤ t ≤ 2 is somewhere between 30 and 36 according to the table we're given in the "Exploration of Riemann Sums" handout. Hmmmm... 2 × 30 = 60 and 2 × 36 =72. Wait, those were the lower and upper estimates for the distance traveled in the first two seconds!
Then, Cal offers another hint:
Close up (error in the light blue):
 |
| Graphic representation of error (in light blue) |
 |
| ABOVE: Lower Riemann Sum = 416 |
 |
| ABOVE: Upper Rieman Sum = 476 |
In conclusion, the basic definition of a Riemann Sum (thanks wiki): "In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral." Foreshadow much?
FINAL THOUGHTS FOR THE DAY:
- At the end of class (the 80-minute period), Mr. O'B handed out IW#6.
- Also, again, it might be a good idea to check out the Riemann Sum applet we used in class.
- Since we didn't get to goal ③ today, we'll work on that tomorrow! P.s. check the 'definite integral' box in the Riemann Sum applet to see what's coming.
*****************************40 minute period (1/30/13)*****************************
For starters, we all went to this site to begin a discussion about what a definite integral is.
We talked even more about INTERVALS. Again, the more intervals a graph has (number of intervals, by the way, is represented by the variable n in the Riemann sum applet), the more accurate the Riemann sum is (i.e. the less error it has). The more intervals a graph has, the closer the Riemann sum over those particular intervals gets to the value of the definite integral.
"If you want the actual true, precise distance that's traveled here, or the precise area that's underneath [this graph on this specific interval of x values], the first semester calc concept you need to take more and more and more rectangles is the..."
LIMIT. That is, if you take the limit of a function as the number of rectangles (aka intervals) goes to infinity, you get the definite integral. Another way to think about the definite integral is the product of x and y, for a continuous function where the y value is not constant (i.e. the y value varies or changes).
Let's talk notation.
We already know that the notation for an indefinite integral a.k.a. an antiderivative is:
But, today we learned that the notation for a definite integral is different. It looks like this:
The a represents the lower limit, and the b represents the upper limit.
Later, we worked on how to find definite integrals using our calculators. Turns out, our calculators already have this function called fnInt, which finds the definite integral for you. Clearly, our class thought this was pretty neat:
TO-DO list:
IW#6
FRQ supercorrection -- how's that graded?
- are you using wolfram alpha?
- are you using Geogebra (graphic, numeric, algebraic)?
Answers for FRQ SUPERCORRECTION (due Friday-- make sure to do this-- we'll learn to do the same problem using the fnInt function on our calculators in class!):
a) -0.524
b) both correct! justify w/ v and v'
c) 2.387
d) 3.423
That's it for now! -Anna
P.s. Chelsea is the next scribe.
***********************************U P D A T E***********************************
Now that we all now about definite integrals, check out this cool applet to play around with definite integral properties. Be sure to check out the "Launch Presentation"button at the bottom of the page to make the applet a separate window!
Even months after learning about Riemann Sums, they're still useful to think about! However, now that we've gone over volume of revolution, we can think of a single slice of a Riemann Sum as the radius of a 3d object, rotate that radius (and the other radiuses of the other slices) around an axis, and come up with some pretty crazy looking three dimensional objects. If you still don't quite see the connection, check out Patrick JMT talking about the volume of revolution using the "washer" method (better known in OB's AP Calc as the "bagel-chip" method. Now, instead of slicing a two dimensional object to estimate the area under a curve, we're considering how to take a slice, use it as a radius, and figure out the volume of the area between two or more curves rotated around an axis!
Best of luck everyone!







Wow, Anna, wow! Very, very impressive!
ReplyDeleteThanks!!
DeleteThis comment has been removed by the author.
ReplyDelete