Even as your faithful scribe was scribbling the last few finishing strokes on his quiz, OB was up front with that special gleam in his eye - you know the one. No, not that one. Yeah, that one. The gleam of intrigue, the one that says we were going to learn something new that day - joy oh joy! I hastened quickly to my seat so as to not miss a second of class time.
We began with a little light math-related humor: }{n}=6)
What is the significance of this equation, you wonder? Why is the limit necessarily six?
Well, let's do some high-level computation. If you cancel the n on the bottom of the fraction with the n on top, the answer obviously becomes =six) . It's so simple! Math really is easy!
. It's so simple! Math really is easy!
When OB cracked this joke, there was an uproar the likes of which have never been heard in the halls of CHRHS before, and likely never will again. All were doubled over in laughter, many struck to the floor, unable to move from the sheer force of the heaving guffaws they produced. There was so much knee-slapping and raucous chortling that the door cracked in five places and several of the support beams in the school's framework vibrated out of place, causing what I suspect to be irreparable damage to the structure. The windows were blown out with the sheer force of the noise, and the lights overhead all exploded in a rain of glass and sparks from the force of the air expelled by a class laughing uproariously in unison.
As we collectively bowed our heads and furiously cogitated over the answer, Duncan beat out Cole by fractions of a second and presented the answer =\frac{1}{3}x^{3}+\frac{4}{3}) . Could this be true? Let's backtrack - if we take the derivative of this function by multiplying by the power of the cubed x and dropping it by one, we get . Success! Does the function go through (2,4)?
. Could this be true? Let's backtrack - if we take the derivative of this function by multiplying by the power of the cubed x and dropping it by one, we get . Success! Does the function go through (2,4)? 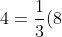+\frac{4}{3}) , it checks out! Once again, Duncan amazed us all with his math expertise.
, it checks out! Once again, Duncan amazed us all with his math expertise.
The example we saw in the above picture is a perfect example of an antiderivative problem - a problem involving finding a function by going backwards from its derivative.
The antiderivative, it should be noted, is not unique until a condition is put on it. In the above problem, the condition of passing through (2,4) was necessary, otherwise there would be a huge set of functions which are the antiderivative of the derivative =x^{2}) shown above. In order to answer the above problem and be just as amazingly well-versed as Duncan, simply look at the problem in the sense of "what would we need to do in order to create a derivative with a squared x in it?" We know how to drop multiply and drop powers in order to find a derivative - what function must we be dealing with then? It has to have
shown above. In order to answer the above problem and be just as amazingly well-versed as Duncan, simply look at the problem in the sense of "what would we need to do in order to create a derivative with a squared x in it?" We know how to drop multiply and drop powers in order to find a derivative - what function must we be dealing with then? It has to have  in it, so that when the power is multiplied in front and dropped, we wind up with an x squared.
in it, so that when the power is multiplied in front and dropped, we wind up with an x squared.
From here, we just plug in our (2,4) point and find... wait... . But that's not right! There must be something added to this equation we're finding; something that, when derived, drops out. Something like a constant - lets call it c.
. But that's not right! There must be something added to this equation we're finding; something that, when derived, drops out. Something like a constant - lets call it c.  . Now this is looking better! What, when added to
. Now this is looking better! What, when added to  , makes 4? Why,
, makes 4? Why,  of course! It seems we found our c! From there, its as simple as putting together the parts and coming up with Duncan's
of course! It seems we found our c! From there, its as simple as putting together the parts and coming up with Duncan's =\frac{1}{3}x^{3}+\frac{4}{3}) . Wasn't that a blast? A gas? A lark? Well, it was something.
. Wasn't that a blast? A gas? A lark? Well, it was something.
Just to beat the idea into the ground, here's a few more examples. Let's say we have =sin(x)) . What is our f(x)? Working backwards, we antiderive (fancy word) that, in order to get sin(x) as a derivative, we must have started with
. What is our f(x)? Working backwards, we antiderive (fancy word) that, in order to get sin(x) as a derivative, we must have started with =-cos(x)) . It only makes sense - since the derivative of cos(x) = -sin(x), this function would give us the desired derivative. But let's step up the math. Take a look at this example:
. It only makes sense - since the derivative of cos(x) = -sin(x), this function would give us the desired derivative. But let's step up the math. Take a look at this example:
How did we know that =tan^{-1}(x)+c) ? Lets remember our definition of the derivative of inverse tan that we all obviously remembered perfectly on the followup!
? Lets remember our definition of the derivative of inverse tan that we all obviously remembered perfectly on the followup! 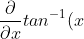=\frac{1}{x^{2}+1})
We know that we may well have a constant c which dropped out of the equation when it was derived, as the example before this one showed us. Thus, we are able to find a function to fit our derivative through the wonders of the antiderivative! Now let's do it again!
Do you follow what the example does? We know that when x is on the bottom of a fraction, that it can be written as being raised to a negative exponent. In this case,  . Using the knowledge Duncan showed so excellently in our first example, lets examine what our function should look like! To get a final value of
. Using the knowledge Duncan showed so excellently in our first example, lets examine what our function should look like! To get a final value of  , we will need a function which, when its exponent is multiplied out in front and then dropped by one, will end up as our desired derivative.
, we will need a function which, when its exponent is multiplied out in front and then dropped by one, will end up as our desired derivative.  fits well! Dropping down a negative one will make the derivative positive, and the power will descend to -2! But we know that a negative powers moves our x to the bottom of the fraction, leaving the -1 on top. Don't forget that there might be a constant c!
fits well! Dropping down a negative one will make the derivative positive, and the power will descend to -2! But we know that a negative powers moves our x to the bottom of the fraction, leaving the -1 on top. Don't forget that there might be a constant c!
Confused? So was I! But then OB in his magnanimity decided to show the problem from another angle so that we might truly master its finer qualities. Let's use the natural log to get the same answer - just from a different angle!
We know that the derivative of ) is
is 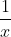 . In this case, the thing on the bottom of the fraction is an
. In this case, the thing on the bottom of the fraction is an 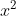 . Thus, we know that it must be what was initially natural log'd. Don't forget that constant c! Work backwards from the f(x) we found above if you're still confused - you'll see that taking its derivative works out. Oh wait... does it? When you bring the power out front, that function becomes
. Thus, we know that it must be what was initially natural log'd. Don't forget that constant c! Work backwards from the f(x) we found above if you're still confused - you'll see that taking its derivative works out. Oh wait... does it? When you bring the power out front, that function becomes +c) . Its derivative wouldn't be what we're looking for, it would be
. Its derivative wouldn't be what we're looking for, it would be  , not
, not 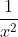 like we wanted! Oh woe and sadness, whatever will we do? We could try dividing by 2...
like we wanted! Oh woe and sadness, whatever will we do? We could try dividing by 2...
No, that doesn't work. What if we squared it?
Well isn't that an interesting idea... What would that give us? It seems we would need the product and chain rules to fix this mess! This means 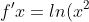*ln(x^2)) . Thus, using the product rule we know that
. Thus, using the product rule we know that 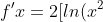*ln(x^2){}']) . However, this is as far as we can go. There is only one antiderivative that can be found per equation, they are unique. MIT to the rescue again!
. However, this is as far as we can go. There is only one antiderivative that can be found per equation, they are unique. MIT to the rescue again!
*******************************************************************************
We have light homework tonight - IW 3 consists of only 8 problems! However, we do have a quiz next class covering IW's 1, 2 and 3, so if you haven't done 1 and 2 yet, get on them!
To wrap up class, we began an explanation of the Mean Value Theorem which we will have to finish for homework. This theorem, like this intermediate value theorem and extreme value theorem will be useful for reasons to be explained in the examination sheet we have for homework. While at the moment we aren't linking derivatives and integrals, we will be doing so in the future. When we get there, this theorem will be invaluable.
Let's look at the mean value theorem from a simplified perspective - say you're driving to Augusta from Camden, and you want to average a speed of 50mph for some reason only known to math problem creators. On the trip, at some point your instantaneous rate of speed must hit 50 mph. You may travel half the trip at 1 mph, but in the middle of your ride your speed must increase at an infinitely quick rate so that you can cover the other half at 99. Even when you jump from 1 to 99, your speed passes through 50mph at some point in time. If you're doing a more modest 40mph for half the trip, you must speed up so that your speedometer passes through 50 to reach 60 for the second half of the trip to average out at 50mph.
Here we see the secant line in red connecting the two endpoints of the segment we are studying - call it [a,b] - and the tan line in blue which is parallel to the secant when taken at some point c. OB seems interested - but why is that? As always, Wikipedia has all the answers to life. But why is this so? The exploration will show us.
Doesn't this remind you of something? Something that starts with an I? Something that starts with an Intermediate? Something that sounds like... shmitermediate shmalue shmeorem? Thats right! It does look like the Intermediate Value Theorem! You're so smart!
Looking at example 1 on the exploration quickly, we notice that there is indeed a point on the interval examined with has a tangent parallel to the secant line drawn between the two endpoints. It seems like the mean value theorem may well hold up. What does Gabe's head have to say about question 2?
Yes Gabe, I agree! It is interesting that its possible for there to be more than one point on a function which has a tangent parallel to a secant drawn between two endpoints of a section.
Alright everyone, make sure that you have the IW's finished tonight as well as the Mean Value Theorem sheet; rest up for the quiz tomorrow also, and don't let those mean values get you down. 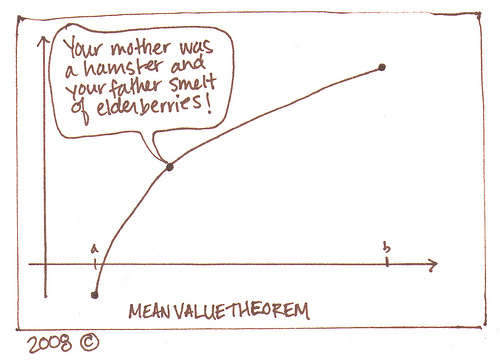












No comments:
Post a Comment