We began class today with a 40 minute quiz on IWs #1-3. Next we read over Rebecca's scribe post, and then Mr. O'Brien talked to the class about the Math Team (for more information about the Math Team click here).
Goals for Today:
- learn how to solve problem c) (below) algebraically
- understand indeterminate forms
- understand the Sandwich Theorem
We were allowed to use our calculators on the following warm up problems (answers included):
a)
b)
c)
Then Mr. O'Brien posed the question: Can limits be done without technology?
We talked about rational functions and their asymptotes, and the way to identify if a rational function has asymptotes. It is important to note that you get an asymptote when you are approaching zero in the denominator of the fraction, and not in the numerator of the fraction. When you divide by a very small number, the fraction gets "explosively" large (e.g. 6 divided by 1 = 6, 6 divided by 0.1 = 60, 6 divided by 0.01 = 600, etc.). If you type 6/0 (or -6/0!) into the Google Calculator, instead of returning "Error", it will give return the answer "Infinity", because the fraction can become infinitely large depending on how close the denominator is to 0. The same thing applies if the denominator approaches zero from the negative side (e.g. 6 divided by -1 is -6, 6 divided by -0.1 is -60, 6 divided by -0.01 is -600, etc.), because the fraction can go to negative infinity as well, still depending on how close the denominator value is to zero.
If the denominator is a constant, and the numerator goes to zero, then the limit will be zero (as zero over any constant is equal to zero).
Then we talked about what happens when you divide zero by zero. If a fraction is approaching zero on the top and zero on the bottom, it is an indeterminate form, which can be defined as "a mathematical expression that is not definitively or precisely determined" (mathworld.wolfram.com). Check out a quick web page from mathworld.wolfram.com on indeterminate forms here!
The Sandwich Theorem (aka the Squeeze Theorem):
Let's look at a basic example of the Sandwich Theorem, using the following equation:
We'll graph it on Geogebra, with h(x) in green, g(x) in red and f(x) in blue.
According to the Sandwich Theorem, the limit g(x)=xsinx should be the same as the limit f(x) and h(x) as x goes to 0...
Finally, here are some things that we went over pertaining to tonight's homework. Mr. O'Brien said that we would be proving that (sin(x))/x =1 in problem 77. To show why this is useful, we worked on these two problems using :
a)
b)
Other Notes:
- IW#4 is only five problems (p.66/ 31, 33, 65, 72, 77) but it's especially important that we try problem #77 for next class.
- Subscribe to the iCal for this class by following the directions on this page.
- The scribe for next class will be Chelsea.
-Anna
UPDATE! Notes on Problem 77:
First of all, here are the notes from the board in today's class. See if you can follow along.
 |
| Note that this triangle uses OPQ which is different than the book's requested triangle OAT (problem #77). |
 |
| Above is the book version of problem #77 on page 68. |
 |
| Please excuse the blurry arm in the picture! |
If you'd like to see another (extremely similar!) proof, check out this video from Khan Academy. In a hurry? You can skip to 4:00 (the first four minutes of the video are mostly spent setting up the diagram provided in problem 77 in our books).
Hope this helps!
-Anna
UPDATE! (Part 2)
Hi again everyone,
Now that we're onto finding the derivative of the functions, I thought I might make a second update to tie between derivatives and limits. As you'll recall, the definition of a derivative has limits in it!
Check out this video from my dear friend patrickJMT on using the derivative definition (h → 0 form) to find a derivative using limits. This should also be helpful for studying for the test next Monday. The main idea of the h→0 form is to algebraically change the fraction:
to make it so the denominator doesn't equal zero (if you're stuck, consider trying to multiply the equation by a conjugate fufoo).
-Anna









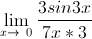








No comments:
Post a Comment