Integration by partial fractions can be difficult - it's a good thing we're here to help. Let James and Alex guide you through the tricky world of partial fraction decomposition as it pertains to integrals.
We begin with a difficult example of a function to integrate: let's say you wanted to find something like:

Looks time-consuming, no? Well, there is a way to more easily reduce integrals via the magic principle of decomposition! Decomposition of a fraction is the process of breaking down more complex equations into their component parts. The first thing you should know is that this method of integration is based off an old algebra trick, simply applied to calculus. We all know the
Fundamental Thorem of Algebra which states that all polynomials can be factored into linear, irreducible quadratic and/or complex (containing imaginary components) factors. This means that polynomials will always have roots which are either linear (such as x+4, x-7, or 12x etc) or are irreducible quadratics which when "reduced" are shown to be made themselves of factors which contain imaginary numbers, always in pairs. Let's say we're not getting into imaginary numbers in our integrating, and we are happy with leaving our decomposed polynomials in terms of their basic building blocks - linear and irreducible quadratic factors.
An important note, however, is that this method about to be described only applies to equations being integrated who take the form of a fraction (technically all equations are fractions) but with the caveat that the denominator (bottom) of the fraction must have a higher power of x than the numerator (top). In cases where the function being integrated has a higher degree numerator, simple long division of your integral will suffice to find your answer.
Lets look at the denominator of the above integration.
The reducible quadratic

shown in the bottom of the fraction being integrated above is factored into its component parts, two
linear factors (x+3) and (x-2). This is nothing new - we've been factoring polynomials for a long time now. Our new integral looks like this:
This is the first of the four major cases which apply to integration by partial fractions - the decomposition (breaking down into factors for easier integration) of Distinct Linear Factors (when the fraction denominator being decomposed breaks down into simple linear factors).
1. Take a look at the following equation and see if you can follow the logic involved.
Why have these constants A and B suddenly been introduced to this process? For the equation in question, it is necessary for some value of A and B to exist so as to make the equality above an accurate statement, right? Some A must exist and some B as well which make this a true statement since the denominators of the two parts of the second side of the equality are factors of the first. We'll demonstrate with a very simplified version of this rule:
If we suppose

, this makes sense right? We know that

.
If we multiply both sides by a funny form of one, we can create a common denominator to match the one we factored apart. When we do this we can see that the above equation is true.
Lets apply this simple rule to our more complex function being integrated. We'll use the same multiplication by one strategy to create a common denominator, and use that to create a more simple form of our function so as to integrate without as many problems - we'll be decomposing it.
(x-2)}=\int%20\frac{A(x-2)}{(x+3)(x-2)}+\frac{B(x+3)}{(x-2)(x+3)})
...all dx, of course.
So how does this help us? Well, now both sides of our equation share the same denominator - let's take it right out. Also, lets drop the integration brackets. They're obscuring our goal right now - to find the values for those two constants A and B and create a more simple equation in order to integrate.
Now, we made a fairly large leap of faith in beginning this problem - mostly, that this equation we're using is differentiable. If we continue to hold this to be true, we assume that this equation we have just found is an identity, meaning that it is true for all values of x in order to be a continuous function which can be integrated at all points.
If we can plug in any x value and be given a correct result in this equation, we can use this to our advantage! Lets cheat the system! The following is a means of performing fractional decomposition which does not work in every circumstance - its a trick like the "drop the power" rule for differentiation, as it only works in simple cases like Case 1 - Distinct Linear Factors. Lets plug in x values which will result in answers for A and B. Try plugging in x=2
Thus, we know now that B = 2/5
Lets do the same strategy for A: say that x = -3
Likewise, we now know that A = 3/5
Now, lets use this knowledge to decompose our origional integral!

and thus, plugging in our values,

This is actually

, as the now defined A and B are constants.
The new form of the original integral we've found is much easier to integrate now. By using the rule of
the integral of 1/x, and remembering that this integral does not have set limits and thus requires a +C, we find the answer to be:
From that messy fraction integral, we have produced an answer! Nice job!
This trick of setting things equal to zero by exploiting the identity of the function we are using can also be applied to problems which belong to Case 2: repeated linear factors. When you see functions which you need to integrate which contain linear functions as the factors of their denominator, but which are repeated more than once, you approach the problem in much the same way.
How would you go about attacking this?
Use the same approach as before, making sure to take into account all possible factors of the denominator. This denominator has many more factors than our original easy example - let's see if we can't find them all.
The parts which go into this function's denominator are (x+1) and (x), yes, but don't forget that its also true that a root for this function is (x+1)^2 and (x+1)^3 as well. With this knowledge, we can set up our decomposed series of fractions. Again, we drop the integral sign for the sake of clarity, and will pick it back up later when we actually solve the integral.
Are you seeing a pattern so far? The fractions we use are comprised of the factors of the bottom of the original function, with letter placeholders over each one which represent constants we will solve for. Integration by partial fractions is a long and painstaking process, but its most important feature is that it yields results. You can probably see how we would go about answering this problem: multiplying by forms of one in order to create one single denominator, then substituting in values of x to isolate constants and solve. Then, we plug in values and perform integration just like the first time.
Now, lets look at the other two cases which are possible in this method. So far, we've been dealing with distinct linear factors, but Case 3 - Distinct Quadratic Factors and Case 4 - Repeated Quadratic Factors are more difficult to solve as they are often at least semi-immune to this trick we've learned so far. So, let's learn the one true (yet painfully slow) method of reducing these equations down. It starts a lot like all the other forms of decomposition, by breaking down the denominator into fractions bearing the parts of said denominator. In Case 3, we see equations like
(x^2+9)}%20=%20\frac{Ax+B}{(x^2+4)}%20+%20\frac{Cx+D}{(x^2+9)})
Notice first off that the denominator is made of irreducible quadratics, aka quadratics which can't break down into linear functions without involving the use of imaginary numbers. Thus, they must remain in the form they are in. Why, you may ask, have the simple constants of A and B become so complicated in this new form, with x's and all? When broken apart in this manner, these equations containing quadratic factors must contain generic linear factors with generic terms like A and B and C and D on top instead of even simpler constants, since these denominators must be one degree greater in power than the numerator which they are underneath. When we were only dealing with linear factors, our numerators were one power less than them, having x's raised to the 0 instead of to the 1. Now, we've raised all the powers by one. Case 4 takes this idea to yet another level in much the same relation that case 1 had to case 2. A sample case 4 problem would look like this:
^3(x^2+9)})
Just like in case 2, we approach this problem by finding all possible factors and creating a decomposition which reflects them.
Now, this is much more complicated a setup than we've had to deal with so far. Let's learn the principle which will serve us better for these more complicated quadratic decompositions. Our trick works well for easier equations, but there is a longer and more time-consuming method which will work every time.
We'll use an easy example: let's refer to our
original original equation way back in case 1 which told us that the following relationship was valid.
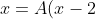+B(x+3))
We will now put a name to this new process - it's called Equating Coefficients. First, we multiply our A's and B's in.
Now, let's look at the invisible exponents in front of our x.
This is where the equating of the coefficients comes into play: since these two identities are equal to each other, the coefficients of each x^1 should equal out, as well as the coefficients of the x^0. This way, we know that 1 = A+B, and that 0 = 2A+B
We now have two true equations, which can be solved any number of ways - the chief two being either equating of equations, or substitution. We'll demonstrate both.
1 = A+B 1-A = B
- 0 = 2A+B 0 = 2A + (1-A)
____________
1 = -A
A=-1, substitute back in to find B = 2
Are these answers familiar? They should be, they're the exact same answers we found for this example when we did it via our little trick! Equating coefficients is longer and more time-consuming, but will never fail you. Combine it with the trick (for finding of easily-identified coefficients) in order to get to the values you're looking for, and decompose your function into a more easily-integrated form. If you want any practice,
UC Davis has 10 problems which they explain well, which will help you practice the basics.
 using the Taylor series.
using the Taylor series.  and it's Taylor approximations, polynomials of degree 1, 3, 5, 7,9, 11 and 13.
and it's Taylor approximations, polynomials of degree 1, 3, 5, 7,9, 11 and 13.


